Elliptic Curve Cryptography

Elliptic Curve

$$y^2 = x^3 + ax + b$$

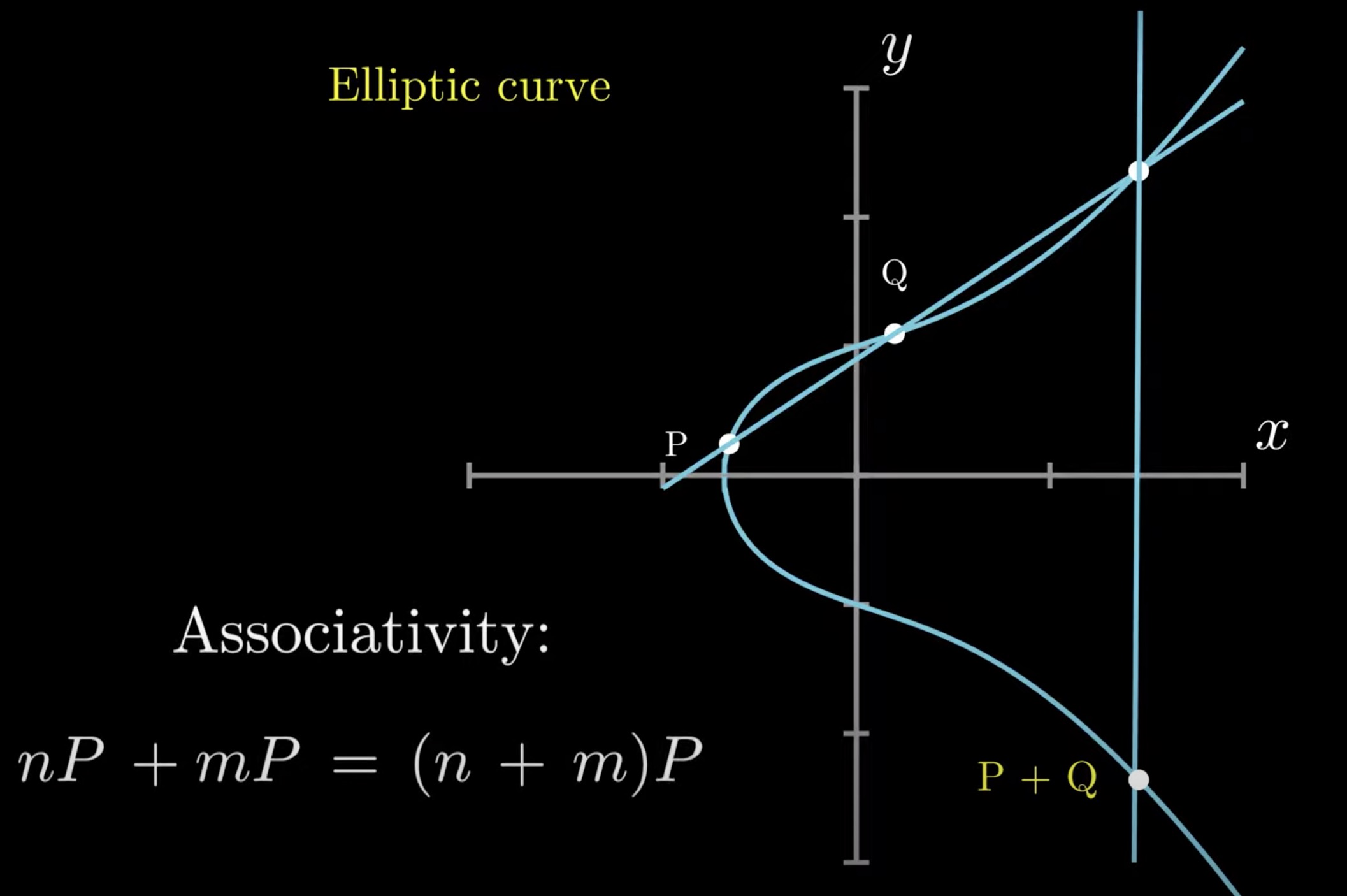
Point Addition

• The point has to be reflected on the x-axis to keep the associactivity of addition

  

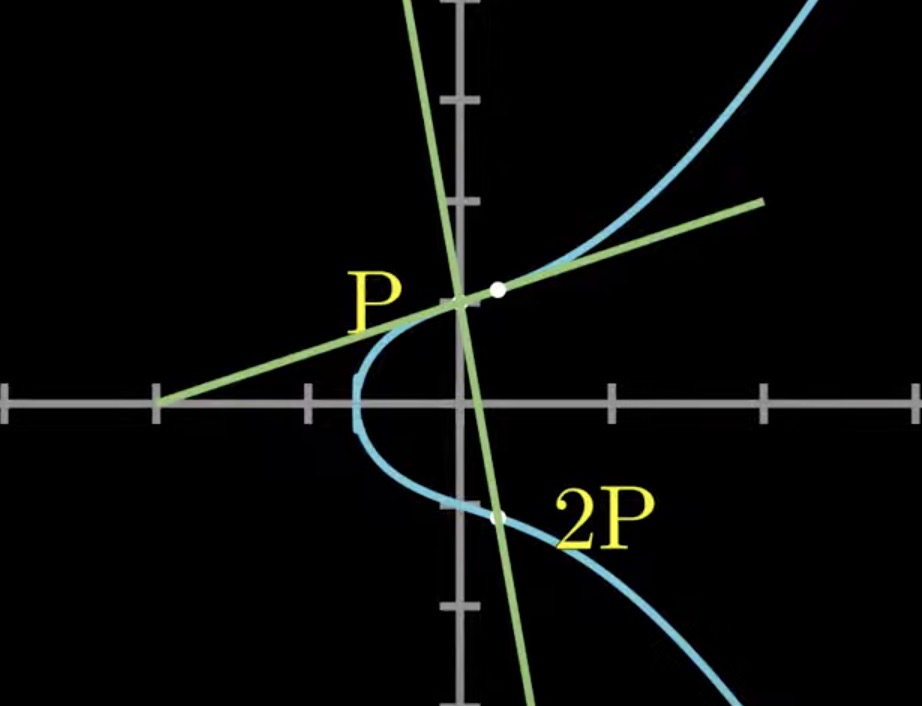
Point Doubling

• Naturally consider the tangent line

  

Elliptic curve cryptography

• To guess the private key $n$ is super super hard

  

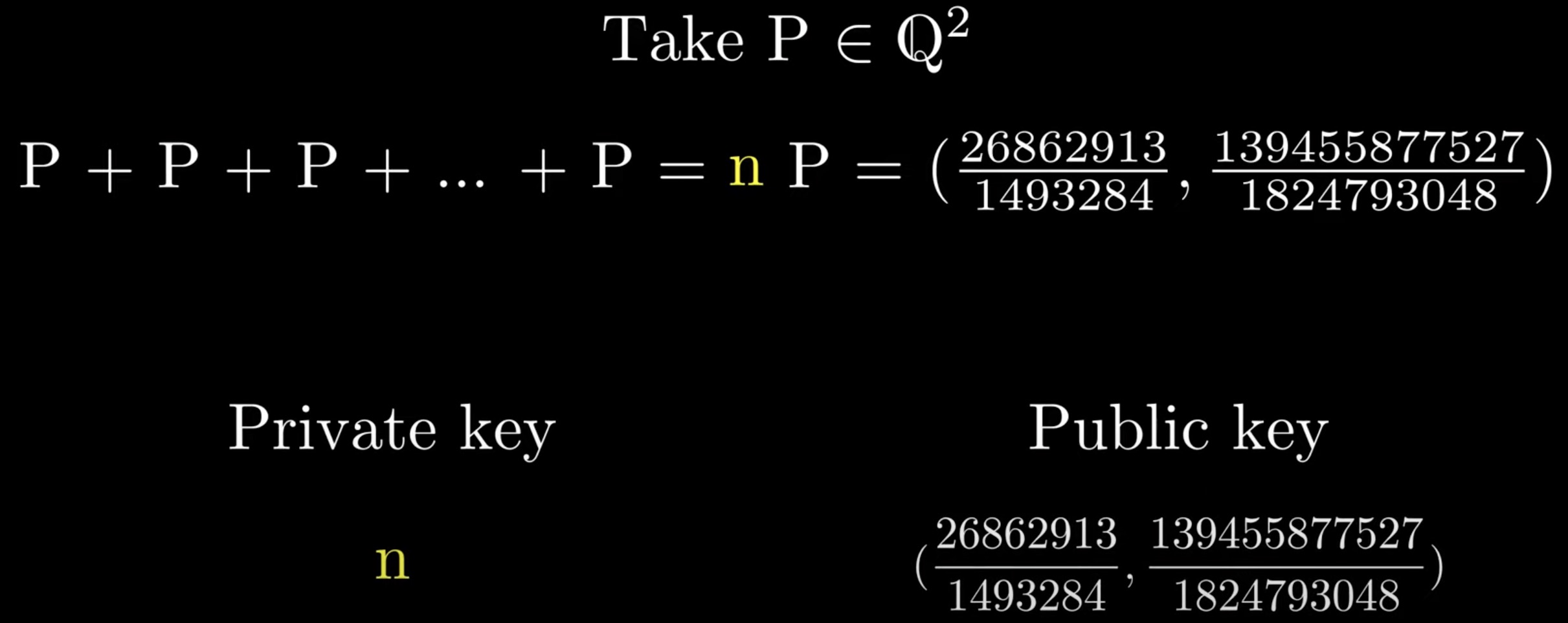
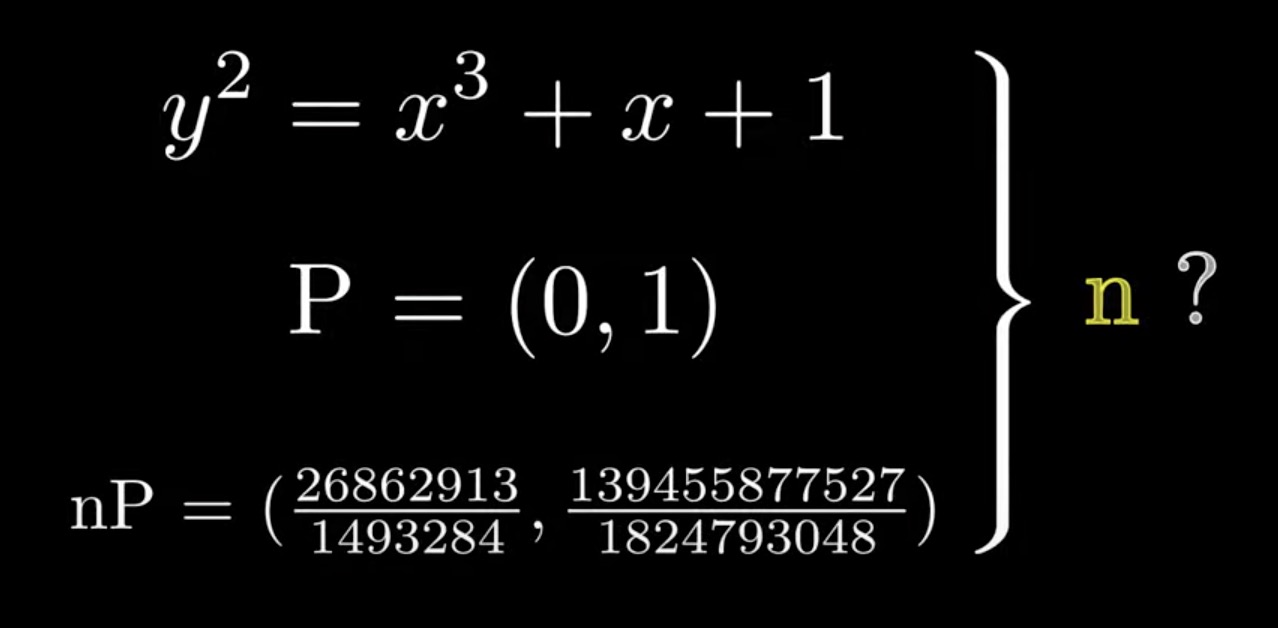
The problem of elliptic curve over real numbers

• The consecutive points of curve $y^2 = x^3 + x + 1$ with the beginning point $(0,1)$ are as follows. For just few steps, the numerator or denominator are going to be too large for computers

  

Elliptic curve over finite field

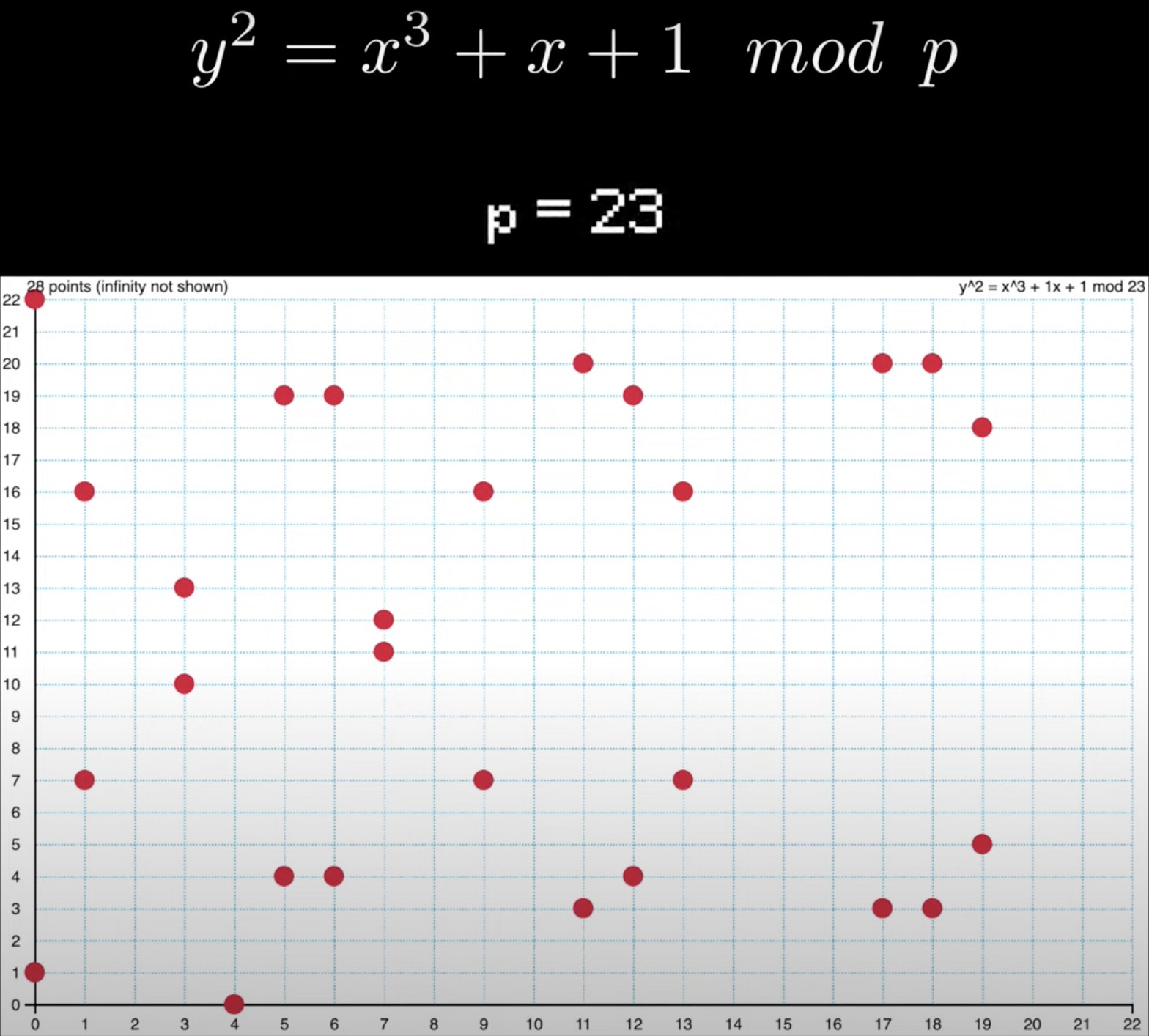
How to calculate the public key

Double-and-add algorithm

• Suppose private key $k=13$ and given the start point $G$. The steps of calculating the public key $13⋅G$ is as follows. What is supposed to be mentioned is that the intermidiate resutl of each step has been calculated

  

Point addition

• Take secp256k1 curve as an example:

$$\begin{cases}y^2 = x^3 + 7 \\ y = ax + b \end{cases}\Rightarrow x^3-a^2x^2-2abx+7-b^2 = 0$$

• According to the Vieta’s formulas

  $$x_3 = a^2-x_1-x_2 \bmod p$$

  then reflect $y_3$

  $$y_3^\prime = -ax_3-b \bmod p$$

  where $a = \frac{y_1-y_2}{x_1-x_2} \bmod p$, $b=y_1-ax_1 \bmod p$.

Point doubling

• According to the point addition section, $x_1=x_2$, $y_1=y_2$ and

  $$a = 3x_1^2 (2y_1)^{-1} \bmod p$$

Since $3 \times 5 \bmod 7 = 1$, $3$ and $5$ are modular inverse for each other with modulo $7$.

Elliptic curve for bitcoin

• The curve equation, prime order of the elliptic curve and the x-coordinate of the base point are as follows.

  

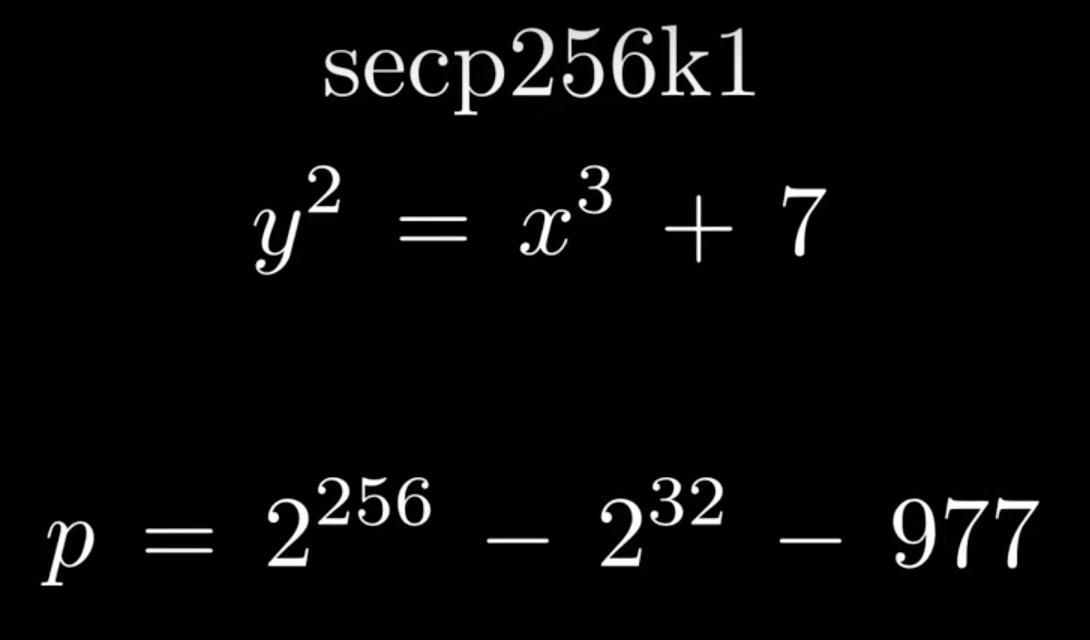
ECDSA (Elliptic Curve Digital Signature Algorithm)

• Sign (how to calculate signature $r, s, v$)

  • given $d$ (private key), $z$ (message hash), $G$ (base point)
  • choose a random number $k ( 0 \lt k \lt p)$, derive point $R = kG = (R_x, R_y)$
  • $r = R_x \bmod p$
  • $s = (z + rd)k^{-1} \bmod p$
  • $v = R_y \bmod 2$

• Send transaction

  • given $r, s, v, z, G$
  • dervive $R_y$ and $R_y^\prime$ with $r$ and curve ( curve is symmetric)
  • determine one of $R_y$ and $R_y^\prime$ with v, then derive $R$
  • dervive $Q$ (public key) according $sk \equiv z + rd \bmod p \Rightarrow sR \equiv zG + rQ \bmod p$
  • derive from address according $Q$
  • check balance and nonce of from address
  • send transaction

• Verify signature

  • given $r, s, z, G, Q$
  • derive $R$ according $sR \equiv zG + rQ \bmod p$
  • check $R_x \equiv r \bmod p$

• Signature malleability

  • given $r, s^\prime, z, G, Q$, where $s^\prime = p - s$
  • notice that $s^\prime \equiv -s \bmod p$
  • so $R^\prime \equiv -R \bmod p$ according to $(-s)(-R) \equiv zG + rQ \bmod p$
  • so $R^\prime_x \equiv -R_x \equiv r \bmod p$

• RFC-6979

  • $k =$ HMAC$(d, z)$

Given $r = R_x$ and curve, two points $(R_x, R_y)$ and $(R_x, R_y^\prime)$ can be derived, where $R_y + R_y^\prime = p$. It is known that $p$ is a big prime number which is odd. So for $R_y$ and $R_y^\prime$, one is odd and the other is even. Given $v$, the correct y-coordinate is determmined.

If any of $r, s, v, z$ is corrupted, a different from address will be derived. Usually, the address has no balance and the transaction will be rejected.